# Run to create population
+set.seed(2022)
+library(tidyverse)
+population <- tibble(student = 1:10000,
+ grade = c(rnorm(n = 3000, mean= 60, sd = 5),
+ rnorm(n = 7000, mean= 80, sd = 5))) %>%
+mutate(grade = round(grade))
+STAT 201 - Statistical Inference for Data Science¶
Lecture 3: Bootstrapping¶
Attribution: these slides are adapted from Vincenzo Coia's slides
+Today¶
-
+
- Module 3: bootstrapping +
- Module 4: Simulation based confidence intervals +
Reminders¶
-
+
- Late registrants: check your due dates on Canvas +
- Worksheet 1 and 2 grades will be available after the late registration worksheets are due date +
- Tutorials may take some time for TAs to mark +
- Solutions will be posted in your Jupyter Hub +
Midterm 1¶
-
+
Midterm 1 is on Thursday July 18 at 1:30 PM in ESB 1012
+-
+
- 1 hour +
- closed book +
- will be served on Canvas with LockDown Browser +
- one double sided cheat sheet (should be on paper not on your computer!) +
- covers all the material from modules 1 - 4 +
- make sure you have either Chrome, Firefox, or some other browser compatible with all of Canvas functionality. +Sometimes Safari has trouble loading images and math. +
+I will post practice problems for mid-term 1 under Midterm 1 module on Canvas
+-
+
- Double check that your midterm works with LockDown Browser! +
+
Summary of what we've learned so far¶
A central goal of this course: +Estimate a population parameter, along with how certain you are.
+The sampling distribution shows us:
+-
+
- What point estimates are possible (even more: their probabilities of occurring, +too) +
- Where the true parameter is (e.g. for means it lies at the mean of the sampling +distribution) +
Motivation for Today's Topic¶
-
+
The sampling distribution is never known in practice, just as the population +parameter is unknown.
+-
+
- We often don't have the resources to collect infinite number of samples. We can have access to a single sample +
- There are different sample statistics (e.g., percentile, median, variance) where the underlying sampling distribution is unknown (i.e., cannot apply CLT) +
+If we knew the sampling distribution, there would be no need to estimate the +population parameter. Why?
+
+
-
+
- ...Because we can extract the population parameter from the sampling +distribution, and report 100% certainty. +
-
+
- Our goal: to estimate the sampling distribution, and interpret it differently from the +actual sampling distribution. +
Recap¶
+IRdisplay::display_html('<iframe src="https://www.zoology.ubc.ca/~whitlock/Kingfisher/CLT.htm" width=800, height=700></iframe> ')
+What is (non-parametric) bootstrapping?¶
(non-parametric) Bootstrapping is a type of resampling where samples of the same size are repeatedly drawn, with replacement, from a single original sample
+
Question for you: Why don't we just resample without replacement?
+# DEMO: Sampling from the population
+
+set.seed(2022)
+library(infer)
+library(tidyverse)
+
+# Taking ONE sample from the population
+original_sample <- sample_n(population, size = 100)
+
+# distribution of the sample
+original_sample %>%
+ ggplot(aes(grade)) + geom_histogram()
+
+# sample mean
+original_sample %>%
+ summarize(mean(grade))
+## Demo: Take one bootstrap sample
+set.seed(202)
+
+rep_sample_n(original_sample,
+ size = ...,
+ replace = ...,
+ reps = 1)
+Bootstrap distribution¶
-
+
- For each bootstrapped sample, compute the point estimate (e.g., mean GPA) +
- Plot the distribution of these point estimates. +

set.seed(2022)
+# Demo: take multiple bootstrap samples
+set.seed(2022)
+
+
+bootstrap_samples <- rep_sample_n(original_sample,
+ size= 100,
+ replace= T,
+ reps =3000)
+
+bootstrap_sampling_dist <- bootstrap_samples %>%
+ ...(replicate) %>%
+ summarize(mean_grade = ...(...))
+ggplot(bootstrap_sampling_dist, aes(x=mean_grade)) +
+ geom_histogram(binwidth = 0.2, boundary = 0.4, color = "white") +
+ labs(x = "Sample means",title = "Bootstrap distribution")+
+ theme(text = element_text(size = 15))
+Sampling distribution versus bootstrap distribution¶
+set.seed(2022)
+sampling_dist <- rep_sample_n(population, size= 100, replace=FALSE, reps =3000)%>%
+ group_by(replicate) %>%
+ summarise(mean_grade = mean(grade))
+p1 <- ggplot(sampling_dist, aes(x=mean_grade)) +
+ geom_histogram(binwidth = 0.2, boundary = 0.5, color = "white") +
+ labs(x = "Sample means",title = "Sampling distribution")+
+ theme(text = element_text(size = 15)) +
+ geom_vline(xintercept=mean(sampling_dist$mean_grade), size=1.5, color="red") +
+ labs(title = paste("Sampling distribution",
+ ", mean=",round(mean(sampling_dist$mean_grade),3),
+ ", SD=",round(sd(sampling_dist$mean_grade),3)))+ theme(text = element_text(size = 15))
+
+p2 <- ggplot(bootstrap_sampling_dist, aes(x=mean_grade)) +
+ geom_histogram(binwidth = 0.2, boundary = 0.5, color = "white") +
+ labs(x = "Sample means",title = "Bootstrap distribution")+
+ theme(text = element_text(size = 15)) +
+ geom_vline(xintercept=mean(bootstrap_sampling_dist$mean_grade), size=1.5, color="red")+
+ labs(title = paste("Bootstrap distribution",
+ ", mean=",round(mean(bootstrap_sampling_dist$mean_grade),3),
+ ", SD=",round(sd(bootstrap_sampling_dist$mean_grade),3)))+ theme(text = element_text(size = 15))
+p3 <- ggplot(original_sample, aes(x=grade)) +
+ geom_histogram( boundary = 0.5, color = "white") +
+ labs(x = "Grade",title = "Sample distribution")+
+ theme(text = element_text(size = 15)) +
+ geom_vline(xintercept=mean(original_sample$grade), size=1.5, color="red")+
+ labs(title = paste("Sample distribution",
+ ", mean=",round(mean(original_sample$grade),3),
+ ", SD=",round(sd(original_sample$grade),3)))+ theme(text = element_text(size = 15))
+
+p4 <- ggplot(population, aes(x=grade)) +
+ geom_histogram(binwidth = 2, boundary = 0.5, color = "white") +
+ labs(x = "Grade",title = "Population distribution")+
+ theme(text = element_text(size = 15)) +
+ geom_vline(xintercept=mean(original_sample$grade), size=1.5, color="red")+
+ labs(title = paste("Population distribution",
+ ", mean=",round(mean(population$grade),3),
+ ", SD=",round(sd(population$grade),3)))+ theme(text = element_text(size = 15))
+options(repr.plot.width=15, repr.plot.height=10)
+cowplot::plot_grid(p4,p3, p1, p2, ncol=2, align="h")
+Clicker Question: Bootstrap distribution is centered around the population mean¶
A. True
+B. False
+ +
+Why bootstrap is good¶
-
+
- Apply to many sample statistics (means, proportions, median, percentile) +
- Works even when there is no ready formula for a standard error (i.e., sampling distribution is unknown) +
- It doesn't require a normally distributed data +
Why bootstrap is not good¶
-
+
- If the sample is not representative, the boostrap distribution will be biased +
- Does not work well when the original sample size is small +
IRdisplay::display_html('<iframe src="https://wise.cgu.edu/portfolio2/bootstrapping/" width=1000, height=600></iframe> ')
+



 -
-

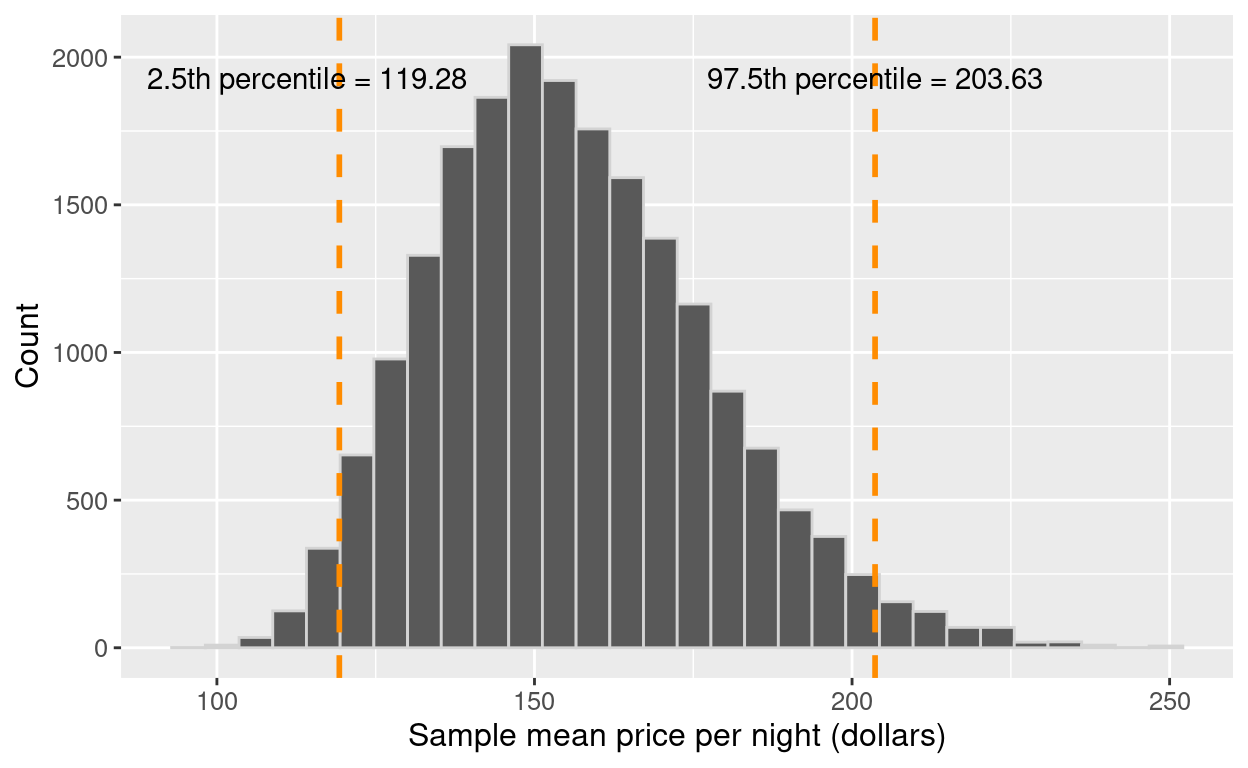
 +
+