Skip to content

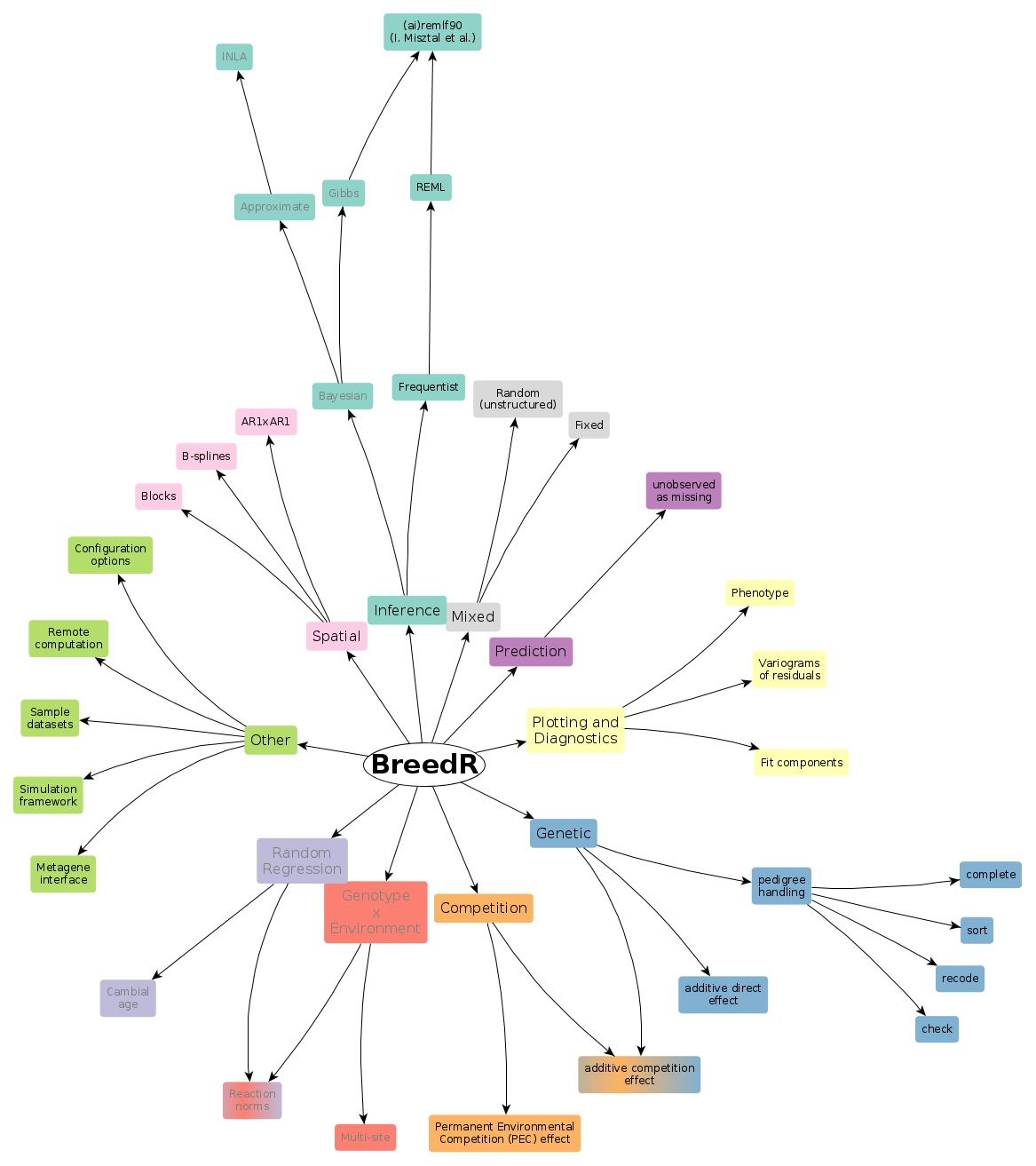
Overview

Jump to bottom Edit New page
Facundo Muñoz edited this page Apr 15, 2017 · 17 revisions

Intro

What is breedR

  • R-package implementing statistical models specifically suited for forest genetic resources analysts.

  • Ultimately Mixed Models, but not necessarily easy to implement and use

  • breedR acts as an interface which provides the means to:

    1. Combine any number of these models as components of a larger model
    2. Compute automatically incidence and covariance matrices from a few input parameters
    3. Fit the model
    4. Plot data and results, and perform model diagnostics

Installation

  • Project web page http://famuvie.github.io/breedR/
    • Set up this URL as a package repository in .Rprofile (detailed instructions on the web)
    • install.packages('breedR')
    • Not possible to use CRAN due to closed-source BLUPF90 programs
  • GitHub dev-site https://github.com/famuvie/breedR
    • if( !require(devtools) ) install.packages('devtools')
    • devtools::install_github('famuvie/breedR')

Where to find help

  • Package's help: help(package = breedR)
    • Help pages ?remlf90
    • Code demos demo(topic, package = 'breedR') (omit topic for a list)
    • Vignettes vignette(package = 'breedR') (pkg and wiki)
  • Wiki pages
    • Guides, tutorials, FAQ
  • Mailing list http://groups.google.com/group/breedr
    • Questions and debates about usage and interface
  • Issues page
    • Bug reports
    • Feature requests

License

GPL-3

  • breedR is FOSS. Licensed GPL-3
    • RShowDoc('LICENSE', package = 'breedR')
  • You can use and distribute breedR for any purpose
  • You can modify it to suit your needs
    • we encourage to!
    • please consider contributing your improvements
    • you can distribute your modified version under the GPL
  • However, breedR makes (intensive) use of the BLUPF90 suite of Fortran programs, which are for free but not free (remember CRAN?)

Roadmap | Future developments

  • Bayesian inference

  • Multi-trait support

  • Genotype×Environment interaction

  • Support for longitudinal data

Functionality

Inference

Frequentist

  • Currently, only frequentist inference is supported via REML estimation of variance components.

  • The function remlf90(), provides an interface to both REMLF90 and AIREMLF90 functions in the BLUPF90 suite of Fortran programs.

  • Type ?remlf90 for details on the syntax

Bayesian

  • It's on the roadmap for the next year

  • Will use a gibbs sampler from BLUPF90, and possibly also INLA

  • The interface will change a bit, separating the model specification from the fit

Linear Mixed Models with unstructured random effects

Example dataset

self dad mum gen gg bl phe_X x y fam
69 0 64 1 14 13 15.756 0 0 64
70 0 41 1 4 13 11.141 3 0 41
71 0 56 1 14 13 19.258 6 0 56
72 0 55 1 14 13 4.775 9 0 55
73 0 22 1 8 13 19.099 12 0 22
74 0 50 1 14 13 19.258 15 0 50 
## 'data.frame':    1021 obs. of  10 variables:
##  $ self : int  69 70 71 72 73 74 75 76 77 78 ...
##  $ dad  : int  0 0 0 0 0 0 0 0 0 4 ...
##  $ mum  : int  64 41 56 55 22 50 67 59 49 8 ...
##  $ gen  : Factor w/ 1 level "1": 1 1 1 1 1 1 1 1 1 1 ...
##  $ gg   : Factor w/ 14 levels "1","2","3","4",..: 14 4 14 14 8 14 14 14 14 11 ...
##  $ bl   : Factor w/ 15 levels "1","2","3","4",..: 13 13 13 13 13 13 13 13 9 9 ...
##  $ phe_X: num  15.76 11.14 19.26 4.78 19.1 ...
##  $ x    : int  0 3 6 9 12 15 18 21 24 27 ...
##  $ y    : int  0 0 0 0 0 0 0 0 0 0 ...
##  $ fam  : Factor w/ 63 levels "6","7","8","9",..: 59 36 51 50 17 45 62 54 44 3 ...

A simple Provenance Test

Specify the genetic group gg as an unstructured random effect using the standard formulas in R

$$ \begin{aligned} \mathrm{phe}_X = & \mu + Z \mathrm{gg} + \varepsilon \\\ \mathrm{gg} \sim & N(0, \sigma_{\mathrm{gg}}^2) \\\ \varepsilon \sim & N(0, \sigma_\varepsilon^2) \end{aligned} $$

res <- remlf90(fixed  = phe_X ~ 1,
               random = ~ gg,
               data   = globulus)
## Using default initial variances given by default_initial_variance()
## See ?breedR.getOption.

Initial variances specification

To avoid the notification, initial values for all the variance components must be made explicit using the argument var.ini:

res <- remlf90(fixed = phe_X ~ 1,
               random = ~ gg,
               var.ini = list(gg = 2, resid = 10),
               data = globulus)

Although in most cases the results will not change at all, we encourage to give explicit initial values for variance components. Specially when some estimate can be artifact. This is also useful for checking sensitivity to initial values.

Exploring the results

summary(res)
## Formula: phe_X ~ 0 + Intercept + gg 
##    Data: globulus 
##   AIC  BIC logLik
##  5864 5874  -2930
## 
## Parameters of special components:
## 
## 
## Variance components:
##          Estimated variances   S.E.
## gg                     2.857 1.3584
## Residual              17.695 0.7888
## 
## Fixed effects:
##            value   s.e.
## Intercept 14.799 0.4911
  • Note that AI-REML has been used by default.
  • You can also specify method = 'em'.
  • Learn about the difference.

Further extractor functions

fixef(res)
## $Intercept
##      value      s.e.
## 1 14.79913 0.4910931

ranef(res)
## $gg
##         value      s.e.
## 1  -1.1113031 0.6582245
## 2  -0.5850024 0.8241561
## 3   1.2381743 0.6017957
## 4  -2.5360692 0.7047331
## 5   1.0223492 0.6298409
## 6  -2.7605955 1.0884704
## 7  -0.5691183 0.9776411
## 8   0.8700425 0.5933964
## 9   1.5572484 0.6381498
## 10 -1.4262287 0.9961138
## 11  1.7715256 0.6527002
## 12  1.8079958 0.8241561
## 13  1.0604393 0.9776411
## 14 -0.3394577 0.5380184

Further extractor functions

qplot(
      fitted(res),
      globulus$phe_X) +
  geom_abline(intercept = 0,
              slope = 1,
              col = 'darkgrey')

str(resid(res))
##  Named num [1:1021] 1.3 -1.12 4.8 -9.68 3.43 ...
##  - attr(*, "names")= chr [1:1021] "1" "2" "3" "4" ...

extractAIC(res)
## [1] 5863.716

logLik(res)
## 'log Lik.' -2929.858 (df=2)

Hierarchical and Factorial models

  • In globulus, the family (mum) is nested within the provenance (gg)

  • This is a matter of codification:

Nested factors

gg mum
A 1
A 2
B 3
B 4

Crossed factors

gg mum
A 1
A 2
B 1
B 2

Model specification

  • Otherwise, in both cases we specify the model in the same way:
random = ~ gg + factor(mum)  # note that mum is numeric
  • Furthermore, this approach can handle unbalanced and mixed designs

Interactions

  • Standard R notation:
random = ~ gg * factor(mum)

  • Not available yet (feature request?)

  • Workaround: build the interaction variable manually

  • Example: gg and block are crossed factors

dat <- transform(globulus,
                 interaction = factor(gg:bl))
random = ~ gg + bl + interaction

Exercise | Hierarchical and Factorial models

  1. Use remlf90() and the globulus dataset to fit

    • a hierarchical model using mum within gg
    • a factorial model using gg and bl

  2. Explore the results with summary()

    • is the family (mum) effect relevant?
    • is there any evidence of interaction between gg and bl?

Hierarchical and Factorial models #1 | Fitting models

res.h <- remlf90(fixed = phe_X ~ 1,
                 random = ~ factor(mum) + gg,
                 data = globulus)
# Interaction variable
globulus.f <- transform(globulus,
                        gg_bl = factor(gg:bl))

res.f <- remlf90(fixed = phe_X ~ 1,
                 random = ~ gg + bl + gg_bl,
                 data = globulus.f)

Hierarchical and Factorial models #2 | Hierarchical model

  • The family effect is not very important, in terms of explained variance
  • However, the model is a bit better with it (AIC, logLik)
summary(res)
## Formula: phe_X ~ 0 + Intercept + gg 
##    Data: globulus 
##   AIC  BIC logLik
##  5864 5874  -2930
## 
## Parameters of special components:
## 
## 
## Variance components:
##          Estimated variances   S.E.
## gg                     2.857 1.3584
## Residual              17.695 0.7888
## 
## Fixed effects:
##            value   s.e.
## Intercept 14.799 0.4911

summary(res.h)
## Formula: phe_X ~ 0 + Intercept + factor(mum) + gg 
##    Data: globulus 
##   AIC  BIC logLik
##  5857 5872  -2926
## 
## Parameters of special components:
## 
## 
## Variance components:
##             Estimated variances   S.E.
## factor(mum)              0.8955 0.4177
## gg                       2.0540 1.1706
## Residual                17.0770 0.7819
## 
## Fixed effects:
##            value   s.e.
## Intercept 14.973 0.4702

Hierarchical and Factorial models #3 | Factorial model

  • Looks like the interaction between block and provenance is negligible
  • (apart from the fact that it makes no sense at all, and shuld not have been even considered in the first place)
  • compare with the model without interaction
summary(res.f)
## Formula: phe_X ~ 0 + Intercept + gg + bl + gg_bl 
##    Data: globulus.f 
##   AIC  BIC logLik
##  5752 5772  -2872
## 
## Parameters of special components:
## 
## 
## Variance components:
##          Estimated variances   S.E.
## gg                   3.10970 1.4329
## bl                   2.57280 1.0606
## gg_bl                0.02912 0.2713
## Residual            15.19800 0.7159
## 
## Fixed effects:
##            value  s.e.
## Intercept 14.764 0.653

## result without interaction
res.f0 <- remlf90(fixed  = phe_X ~ 1,
                  random = ~ gg + bl,
                  data = globulus)
paste('AIC:', round(extractAIC(res.f0)),
      'logLik:', round(logLik(res.f0)))
## [1] "AIC: 5750 logLik: -2872"

Additive Genetic Effect

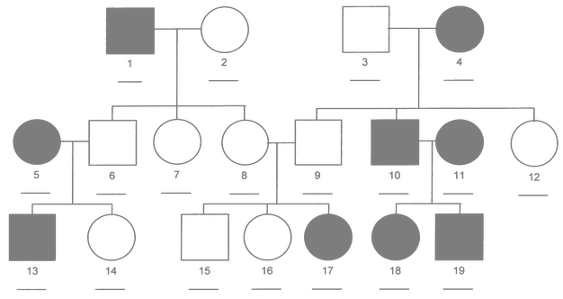
pedigree

What is an additive genetic effect

  • Random effect at individual level
  • Based on a pedigree
  • BLUP of Breeding Values from own and relatives' phenotypes
  • Represents the additive component of the genetic value
  • More general:
  • family effect is a particular case
  • accounts for more than one generation
  • mixed relationships
  • More flexible: allows to select individuals within families

Specifying a pedigree

  • A 3-column data.frame or matrix with the codes for each individual and its parents

  • A family effect is easily translated into a pedigree:

    • use the family code as the identification of a fictitious mother
    • use 0 or NA as codes for the unknown fathers
self dad mum
69 0 64
70 0 41
71 0 56
72 0 55
73 0 22
74 0 50

Fitting an animal model 

res.animal <- remlf90(fixed  = phe_X ~ 1,
                      random = ~ gg,
                      genetic = list(model = 'add_animal', 
                                     pedigree = globulus[, 1:3],
                                     id = 'self'), 
                      data = globulus)

Animal model: results

  • gg explains almost the same amount of phenotypic variability

  • The (additive) genetic effect explains part of the formerly residual variance

  • The heritability is computed automatically as $$h^2 = \frac{\sigma_a^2}{\sigma_a^2 + \sigma_{gg}^2+ \sigma^2}$$

summary(res.animal)
## Formula: phe_X ~ 0 + Intercept + gg + pedigree 
##    Data: globulus 
##   AIC  BIC logLik
##  5857 5872  -2926
## 
## Parameters of special components:
## 
## 
## Variance components:
##          Estimated variances  S.E.
## gg                     2.356 1.249
## genetic                3.632 1.649
## Residual              14.271 1.561
## 
##              Estimate    S.E.
## Heritability   0.1795 0.08253
## 
## Fixed effects:
##            value s.e.
## Intercept 14.797 0.47

Extracting Predicted Breeding Values

## Predicted Breeding Values
# for the full pedigree first, and for the observed individuals
# by matrix multiplication with the incidence matrix
PBV.full <- ranef(res.animal)$genetic
PBV <- model.matrix(res.animal)$genetic %*% PBV.full

# Predicted genetic values vs.
# phenotype.
# Note: fitted = mu + PBV
qplot(fitted(res.animal), phe_X,
      data = globulus) +
  geom_abline(intercept = 0,
              slope = 1,
              col = 'gray')

Handling pedigrees

  • The pedigree needs to meet certain conditions

  • If it does not, breedR automatically completes, recodes and sorts

  • If recoding is necessary, breedR issues a warning because you need to be careful when retrieving results

  • See this guide for more details

Spatial autocorrelation

spatial

What is spatial autocorrelation

  • The residuals of any LMM must be noise

  • However, most times there are environmental factors that affect the response

  • This causes that observations that are close to each other tend to be more similar that observations that are far away

  • This is called spatial autocorrelation

  • It may affect both the estimations and their accuracy

  • This is why experiments are randomized into spatial blocks

Diagnosing spatial autocorrelation | residuals spatial plot

  • You can plot() the spatial arrangement of various model components (e.g. residuals)

  • Look like independent gaussian observations (i.e. noise)?

  • Do you see any signal in the background?

## Since coordinates have not
## been passed before they 
## must be provided explicitly.
coordinates(res.animal) <-
  globulus[, c('x', 'y')]
plot(res.animal, 'resid')

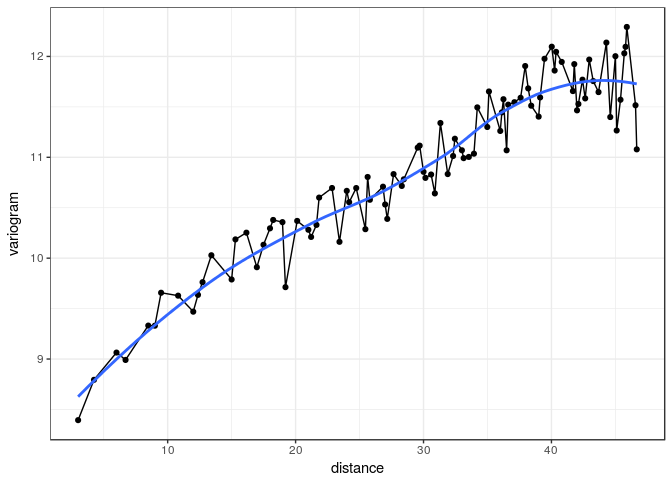
Diagnosing spatial autocorrelation | variograms of residuals

  • Plot the variogram of residuals with variogram() 
variogram(res.animal)

Interpreting the variograms

  • Isotropic variogram: $$ \gamma(h) = \frac12 V[Z(\mathbf{u}) - Z(\mathbf{v})], \quad \text{dist}(\mathbf{u}, \mathbf{v}) = h $$

The empirical isotropic variogram is built by aggregating all the pairs of points separated by h, no matter the direction.

Interpreting the variograms

  • Row/Column variogram: $$ \gamma(x, y) = \frac12 V[Z(\mathbf{u}) - Z(\mathbf{v})], \quad \text{dist}(\mathbf{u}, \mathbf{v}) = (x, y) $$

The empirical row/col variogram is built by aggregating all the pairs of points separated by exactly x rows and y columns.

Interpreting the variograms

  • Anisotropic variogram: $$ \gamma(\mathbf{x}) = \frac12 V[Z(\mathbf{u}) - Z(\mathbf{v})], \quad \mathbf{u} = \mathbf{v} \pm \mathbf{x} $$

The empirical anisotropic variogram is built by aggregating all the pairs of points in the same direction separated by |x|.

Accounting for spatial autocorrelation

  • Include an explicit spatial effect in the model

  • I.e., a random effect with a specific covariance structure that reflects the spatial relationship between individuals

  • The block effect, is a very particular case:

    • It is designed from the begining, possibly using prior knowledge
    • Introduces independent effects between blocks
    • Most neighbours are within the same block (i.e. share the same effect)

The blocks model

# The genetic component (DRY)
gen.globulus <- list(model    = 'add_animal', 
                     pedigree = globulus[, 1:3],
                     id       = 'self')

res.blk <- remlf90(fixed   = phe_X ~ 1,
                   random  = ~ gg,
                   genetic = gen.globulus, 
                   spatial = list(model = 'blocks', 
                                  coord = globulus[, c('x', 'y')],
                                  id = 'bl'),
                   data    = globulus)
  • The blocks spatial model is equivalent to random = ~ bl, but:
    • specifying coord is convenient for plotting (remember?)
    • blocks behaves as expected, even if bl is not a factor

Animal-spatial model: results

summary(res.blk)
## Formula: phe_X ~ 0 + Intercept + gg + pedigree + spatial 
##    Data: globulus 
##   AIC  BIC logLik
##  5734 5753  -2863
## 
## Parameters of special components:
## spatial: n.blocks: 15
## 
## Variance components:
##          Estimated variances  S.E.
## gg                     2.385 1.274
## genetic                5.275 1.836
## spatial                2.650 1.081
## Residual              10.279 1.601
## 
##              Estimate    S.E.
## Heritability   0.2556 0.08989
## 
## Fixed effects:
##            value   s.e.
## Intercept 14.762 0.6342
  • Now the additive-genetic variance and the heritability have increased! (3.6 and 0.18 before)

Variogram of residuals

  • There seems to remain some intra-block spatial autocorrelation

B-Splines model

  • A continuous and smooth spatial surface built from a linear combination of basis functions
  • The coefficients are modelled as a random effect
## Use the `em` method! `ai` does not like splines
res.spl  <- remlf90(fixed   = phe_X ~ 1,
                    random  = ~ gg,
                    genetic = gen.globulus, 
                    spatial = list(model   = 'splines', 
                                   coord   = globulus[, c('x','y')]), 
                    data    = globulus, method  = 'em')

Autoregressive model

  • A separable kronecker product of First order Autoregressive processes on the rows and the colums
res.ar1  <- remlf90(fixed   = phe_X ~ 1,
                    random  = ~ gg,
                    genetic = gen.globulus, 
                    spatial = list(model = 'AR', 
                                   coord = globulus[, c('x','y')]), 
                    data    = globulus)

Change in model residuals

  • We preserve the scale by using compare.plots() 
compare.plots(
  list(`Animal model only` = plot(res.animal, 'residuals'),
       `Animal/blocks model` = plot(res.blk, 'residuals'),
       `Animal/splines model` = plot(res.spl, 'residuals'),
       `Animal/AR1 model` = plot(res.ar1, 'residuals')))

Comparison of spatial components

compare.plots(list(Blocks  = plot(res.blk, type = 'spatial'),
                   Splines = plot(res.spl, type = 'spatial'),
                   AR1xAR1 = plot(res.ar1, type = 'spatial')))

Prediction of the spatial effect in unobserved locations

  • The type fullspatial fills the holes (when possible)

  • See ?plot.remlf90

compare.plots(list(Blocks  = plot(res.blk, type = 'fullspatial'),
                   Splines = plot(res.spl, type = 'fullspatial'),
                   AR1xAR1 = plot(res.ar1, type = 'fullspatial')))

Spatial parameters | Number of knots of a splines model

  • The smoothness of the spatial surface can be controlled modifying the number of base functions

  • This is, directly determined by the number of knots (nok) in each dimension

  • n.knots can be used as an additional argument in the spatial effect as a numeric vector of size 2.

  • Otherwise, is determined by the function given in breedR.getOption('splines.nok')

Spatial parameters | Autoregressive parameters of a AR model

  • Analogously, the patchiness of the AR effects can be controlled by the autoregressive parameter for each dimension

  • rho can be given as an additional argument in the spatial effect as a numeric vector of size 2

  • By default, breedR runs all the combinations in the grid produced by the values from breedR.getOption('ar.eval') and returns the one with largest likelihood

  • It returns also the full table of combinations and likelihoods in res$rho

Exercise | Tuning spatial parameters

  • Tuning parameters:
    • model splines: n.knots
    • model AR: rho

  1. Increase the number of knots in the splines model and see if it improves the fit

  2. Visualize the log-likelihood of the fitted AR models

  3. Refine the grid around the most likely values, and refit using rho = rho.grid, where

rho.grid <- expand.grid(rho_r = seq(.7, .95, length = 4),
                        rho_c = seq(.7, .95, length = 4))
- What are now the most likely parameters?

Spatial #1 | B-splines model with increased nok

  • nok were (6, 6) by default (see summary())
res.spl99  <- remlf90(fixed  = phe_X ~ 1, random = ~ gg,
                      genetic = gen.globulus,
                      spatial = list(model   = 'splines', 
                                     coord   = globulus[, c('x','y')],
                                     n.knots = c(9, 9)), 
                      data = globulus, method = 'em')
summary(res.spl)
## Formula: phe_X ~ 0 + Intercept + gg + pedigree + spatial 
##    Data: globulus 
##   AIC     BIC logLik
##  5685 unknown  -2838
## 
## Parameters of special components:
## spatial: n.knots: 12 12
## 
## Variance components:
##          Estimated variances
## gg                     2.568
## genetic                4.498
## spatial                4.199
## Residual              10.070
## 
## Fixed effects:
##            value   s.e.
## Intercept 14.479 0.9163

summary(res.spl99)
## Formula: phe_X ~ 0 + Intercept + gg + pedigree + spatial 
##    Data: globulus 
##   AIC     BIC logLik
##  5681 unknown  -2836
## 
## Parameters of special components:
## spatial: n.knots: 15 15
## 
## Variance components:
##          Estimated variances
## gg                     2.509
## genetic                4.651
## spatial                3.490
## Residual               9.552
## 
## Fixed effects:
##            value   s.e.
## Intercept 14.611 0.6947

Spatial #2 | Visualize log-likelihoods

qplot(rho_r, rho_c,
      fill = loglik,
      geom = 'tile',
      data = res.ar1$rho)

rho_r rho_c loglik
-0.8 -0.8 -2925.648
-0.2 -0.8 -2925.647
0.2 -0.8 -2925.645
0.8 -0.8 -2925.636
-0.8 -0.2 -2925.647
-0.2 -0.2 -2925.645
0.2 -0.2 -2925.023
0.8 -0.2 -2876.893
-0.8 0.2 -2925.645
-0.2 0.2 -2925.645
0.2 0.2 -2871.691
0.8 0.2 -2849.814
-0.8 0.8 -2925.645
-0.2 0.8 -2890.606
0.2 0.8 -2860.981
0.8 0.8 -2828.017

Spatial #3 | Refine grid

rho.grid <- expand.grid(rho_r = seq(.7, .95, length = 4),
                        rho_c = seq(.7, .95, length = 4))
res.ar.grid  <- remlf90(fixed  = phe_X ~ gg,
                        genetic = list(model = 'add_animal', 
                                       pedigree = globulus[,1:3],
                                       id = 'self'), 
                        spatial = list(model = 'AR', 
                                       coord = globulus[, c('x','y')],
                                       rho = rho.grid), 
                        data = globulus)
summary(res.ar.grid)
## Formula: phe_X ~ 0 + gg + pedigree + spatial 
##    Data: globulus 
##   AIC  BIC logLik
##  5603 5617  -2798
## 
## Parameters of special components:
## spatial: rho: 0.8666667 0.7833333
## 
## Variance components:
##          Estimated variances  S.E.
## genetic                5.090 1.715
## spatial                4.984 1.053
## Residual               7.583 1.499
## 
##              Estimate    S.E.
## Heritability   0.2878 0.09383
## 
## Fixed effects:
##        value   s.e.
## gg.1  13.351 0.7195
## gg.2  14.331 0.9112
## gg.3  15.945 0.7698
## gg.4  11.585 0.9394
## gg.5  15.913 0.8200
## gg.6   9.593 1.6964
## gg.7  13.761 1.5681
## gg.8  15.521 0.7486
## gg.9  16.302 0.8260
## gg.10 12.684 1.1531
## gg.11 16.459 0.9849
## gg.12 16.801 1.1412
## gg.13 15.783 1.5665
## gg.14 14.211 0.6486

Competition

Theoretical model

Competition model

  • Each individual have two (unknown) Breeding Values (BV)
  • The direct BV affects its own phenotype, while the competition BV affects its neghbours' (as the King moves)
  • The effect of the neighbouring competition BVs is given by their sum weighted by 1/dα, where α is a tuning parameter called decay
  • Each set of BVs is modelled as a zero-mean random effect with structure matrix given by the pedigree and independent variances σa2 and σc2
  • Both random effects are modelled jointly with correlation ρ

Permanent Environmental Effect (pec)

  • Optional effect with environmental (rather than genetic) basis

  • Modelled as an individual independent random effect that affects neighbouring trees in the same (weighted) way

Simulation of data

breedR implements a convenient dataset simulator which keeps a similar syntax.

  • See ?simulation for details on the syntax
# Simulation parameters
grid.size <- c(x=20, y=25) # cols/rows
coord <- expand.grid(sapply(grid.size,
                            seq))
Nobs <- prod(grid.size)
Nparents <- c(mum = 20, dad = 20)
sigma2_a <- 2   # direct add-gen var
sigma2_c <- 1   # compet add-gen var
rho      <- -.7 # gen corr dire-comp
sigma2_s <- 1   # spatial variance
sigma2_p <- .5  # pec variance
sigma2   <- .5  # residual variance

S <- matrix(c(sigma2_a,
              rho*sqrt(sigma2_a*sigma2_c),
              rho*sqrt(sigma2_a*sigma2_c),
              sigma2_c),
            2, 2)

set.seed(12345)
simdat <- 
  breedR.sample.phenotype(
    fixed   = c(beta = 10),
    genetic = list(model = 'competition',
                   Nparents = Nparents,
                   sigma2_a = S,
                   check.factorial=FALSE,
                   pec = sigma2_p),
    spatial = list(model = 'AR',
                   grid.size = grid.size,
                   rho   = c(.3, .8),
                   sigma2_s = sigma2_s),
    residual.variance = sigma2
    )

## Remove founders
dat <- subset(simdat,
              !(is.na(simdat$sire)
                & is.na(simdat$dam)))

Fitting a competition model

system.time(
  res.comp <- remlf90(fixed   = phenotype ~ 1,
                      genetic = list(model = 'competition',
                                     pedigree = dat[, 1:3],
                                     id = 'self',
                                     coord = dat[, c('x', 'y')],
                                     competition_decay = 1,
                                     pec = list(present = TRUE)),
                      spatial = list(model = 'AR', 
                                     coord = dat[, c('x', 'y')],
                                     rho   = c(.3, .8)),
                      data = dat,
                      method = 'em')  # AI diverges
  )
##    user  system elapsed 
## 101.684   0.208 101.917

True vs. estimated parameters

True Estimated
direct 2.0 2.50
compet. 1.0 1.03
correl. -0.7 -0.76
spatial 1.0 1.24
pec 0.5 0.20
residual 0.5 0.17

Exercise | Competition models

  1. Plot the true vs predicted:

    • direct and competition Breeding Values
    • spatial effects
    • pec effects

  2. Plot the residuals and their variogram

    • Do you think the residuals are independent?
    • How would you improve the analysis?

Competition #1 | True vs. predicted components

## compute the predicted effects for the observations
## by matrix multiplication of the incidence matrix and the BLUPs
pred <- list()
Zd <- model.matrix(res.comp)$'genetic_direct'
pred$direct <- Zd %*% ranef(res.comp)$'genetic_direct'

## Watch out! for the competition effects you need to use the incidence
## matrix of the direct genetic effect, to get their own value.
## Otherwise, you get the predicted effect of the neighbours on each
## individual.
pred$comp <- Zd %*% ranef(res.comp)$'genetic_competition'
pred$pec  <- model.matrix(res.comp)$pec %*% ranef(res.comp)$pec

Competition #1 | True vs. predicted components

comp.pred <-
  rbind(
    data.frame(
      Component = 'direct BV',
      True = dat$BV1,
      Predicted = pred$direct),
    data.frame(
      Component = 'competition BV',
      True = dat$BV2,
      Predicted = pred$comp),
    data.frame(
      Component = 'pec',
      True      = dat$pec,
      Predicted = as.vector(pred$pec)))

ggplot(comp.pred,
       aes(True, Predicted)) +
  geom_point() + 
  geom_abline(intercept = 0, slope = 1,
              col = 'darkgray') +
  facet_grid(~ Component)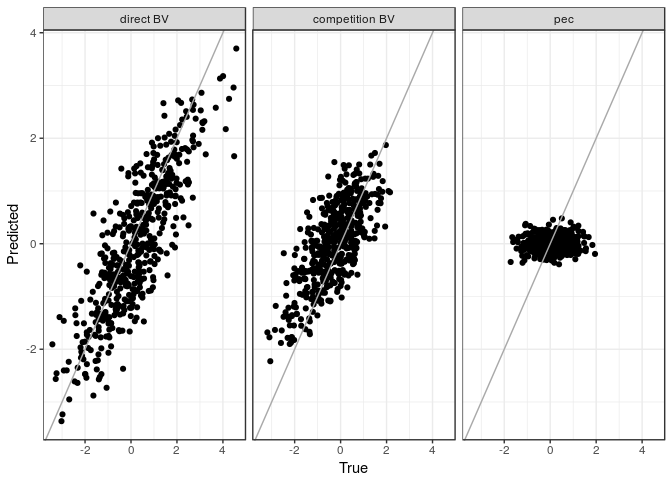

The predition of the Permanent Environmental Competition effect is not precisely great...

Competition #2 | Map of residuals and their variogram

plot(res.comp, type = 'resid')
variogram(res.comp)

Generic component

The Generic model

This additional component allows to introduce a random effect ψ with arbitrary incidence and covariance matrices Z and Σ:

$$ \begin{aligned} y = & \mu + X \beta + Z \psi + \varepsilon \\\ \psi \sim & N(0, \sigma_\psi^2 \Sigma_\psi) \\\ \varepsilon \sim & N(0, \sigma_\varepsilon^2) \end{aligned} $$

Implementation of the generic component

## Fit a blocks effect using generic
inc.mat <- model.matrix(~ 0 + bl, globulus)
cov.mat <- diag(nlevels(globulus$bl))
res.blg <- remlf90(fixed  = phe_X ~ gg,
                   generic = list(block = list(inc.mat,
                                               cov.mat)),
                   data   = globulus)

Example of result

## Formula: phe_X ~ 0 + gg 
##    Data: globulus 
##   AIC  BIC logLik
##  5691 5701  -2844
## 
## Parameters of special components:
## 
## 
## Variance components:
##          Estimated variances   S.E.
## block                  2.592 1.0640
## Residual              15.208 0.6825
## 
## Fixed effects:
##        value   s.e.
## gg.1  13.534 0.6222
## gg.2  14.030 0.8464
## gg.3  16.106 0.5513
## gg.4  11.854 0.6824
## gg.5  15.883 0.5863
## gg.6  10.220 1.3041
## gg.7  13.995 1.0894
## gg.8  15.728 0.5410
## gg.9  16.478 0.5969
## gg.10 12.843 1.1225
## gg.11 16.744 0.6151
## gg.12 17.002 0.8464
## gg.13 16.297 1.0894
## gg.14 14.429 0.4730

Prediction

Predicting values for unobserved trees

  • You can predict the Breeding Value of an unmeasured tree

  • Or the expected phenotype of a death tree (or an hypothetical scenario)

  • Information is gathered from the covariates, the spatial structure and the pedigree

  • Simply include the individual in the dataset with the response set as NA

Leave-one-out cross-validation

  • Re-fit the simulated competition data with one measurement removed

  • Afterwards, compare the predicted values for the unmeasured individuals with their true simulated values

rm.idx <- 8
rm.exp <- with(dat[rm.idx, ],
               phenotype - resid)
dat.loo <- dat
dat.loo[rm.idx, 'phenotype'] <- NA
True Pred.loo
direct BV -1.48 0.11
competition BV 0.46 0.36
exp. phenotype 6.80 9.90

Exercise | Cross validation

  1. Extend the last table to include the predicted values with the full dataset

  2. Remove 1/10th of the phenotypes randomly, and predict their expected phenotype

    • Have the parameter estimations changed too much?

  3. Compute the Root Mean Square Error (RMSE) of Prediction with respect to the true values

Cross-validation #1 | Include prediction with full data

pred.BV.mat <- with(ranef(res.comp), 
                    cbind(`genetic_direct`, `genetic_competition`))

valid.pred$Pred.full <- c(Zd[rm.idx, ] %*% pred.BV.mat,
                          fitted(res.comp)[rm.idx])
True Pred.full Pred.loo
direct BV -1.48 -1.30 0.11
competition BV 0.46 0.99 0.36
exp. phenotype 6.80 7.29 9.90

Cross-validation #2 | Perform cross-validation on 1/10th of the observations

rm.idx <- sample(nrow(dat), nrow(dat)/10)
dat.cv <- dat
dat.cv[rm.idx, 'phenotype'] <- NA
## Re-fit the model and build table
Fully.estimated CV.estimated
direct 2.50 2.69
compet. 1.03 0.86
correl. -0.76 -0.80
spatial 1.24 1.03
pec 0.20 0.51
residual 0.17 0.14

Cross-validation #3 | MSE of Prediction

true.exp.cv <- with(dat[rm.idx, ], phenotype - resid)
round(sqrt(mean((fitted(res.comp.cv)[rm.idx] - true.exp.cv)^2)), 2)
## [1] 1.5

Multiple traits

breedR provides a basic interface for multi-trait models which only requires specifying the different traits in the main formula using cbind().

## Filter site and select relevant variables
dat <- 
  droplevels(
    douglas[douglas$site == "s3",
            names(douglas)[!grepl("H0[^4]|AN|BR|site", names(douglas))]]
  )

res <- 
  remlf90(
    fixed = cbind(H04, C13) ~ orig,
    genetic = list(
      model = 'add_animal', 
      pedigree = dat[, 1:3],
      id = 'self'),
    data = dat
  )
## Warning in build_pedigree(1:3, data = ped.df): The pedigree has been
## recoded. Check attr(ped, 'map').

## Using default initial variances given by default_initial_variance()
## See ?breedR.getOption.

A full covariance matrix across traits is estimated for each random effect, and all results, including heritabilities, are expressed effect-wise:

## Formula: cbind(H04, C13) ~ 0 + orig + pedigree 
##    Data: dat 
##    AIC   BIC logLik
##  30968 31010 -15476
## 
## Parameters of special components:
## 
## 
## Variance components:
##                                       Estimated variances   S.E.
## genetic.direct.H04                                  918.1  438.6
## genetic.direct.H04_genetic.direct.C13              1872.4  824.0
## genetic.direct.C13                                 5827.6 1829.6
## Residual.H04                                       8373.7  461.7
## Residual.H04_Residual.C13                         10922.0  755.3
## Residual.C13                                      18439.0 1484.2
## 
##                  Estimate    S.E.
## Heritability:H04   0.0990 0.04589
## Heritability:C13   0.2391 0.07036
## 
## Fixed effects:
##              value    s.e.
## orig.H04.pA 352.00  6.2389
## orig.H04.pB 370.90 10.7947
## orig.H04.pC 346.93 13.0788
## orig.H04.pF 339.66  6.2268
## orig.H04.pG 313.00 24.0430
## orig.H04.pH 305.39 19.9334
## orig.H04.pI 323.29 20.0946
## orig.H04.pJ 343.87 19.8567
## orig.H04.pK 335.48 19.6409
## orig.C13.pA 460.01 13.6444
## orig.C13.pB 494.58 19.8635
## orig.C13.pC 430.86 25.5477
## orig.C13.pF 429.48 12.5501
## orig.C13.pG 376.42 48.3133
## orig.C13.pH 376.98 43.4266
## orig.C13.pI 404.62 43.6194
## orig.C13.pJ 418.91 43.2856
## orig.C13.pK 441.99 43.0567

Although the results are summarized in tabular form, the covariance matrices can be recovered directly:

res$var[["genetic", "Estimated variances"]]
##            direct.H04 direct.C13
## direct.H04     918.08     1872.4
## direct.C13    1872.40     5827.6

## Use cov2cor() to compute correlations
cov2cor(res$var[["genetic", "Estimated variances"]])
##            direct.H04 direct.C13
## direct.H04  1.0000000  0.8094938
## direct.C13  0.8094938  1.0000000

Estimates of fixed effects and BLUPs of random effects can be recovered with fixef() and ranef() as usual. The only difference is that they will return a list of matrices rather than vectors, with one column per trait.

The standard errors are given as attributes, and are displayed in tabular form whenever the object is printed.

fixef(res)       ## printed in tabular form, but...
## $orig
##    value.H04 value.C13  s.e..H04 s.e..C13
## pA  352.0025  460.0097  6.238914 13.64437
## pB  370.8997  494.5846 10.794693 19.86351
## pC  346.9318  430.8644 13.078774 25.54773
## pF  339.6614  429.4795  6.226796 12.55013
## pG  313.0000  376.4231 24.043034 48.31334
## pH  305.3889  376.9779 19.933367 43.42664
## pI  323.2885  404.6216 20.094619 43.61939
## pJ  343.8727  418.9064 19.856683 43.28562
## pK  335.4828  441.9861 19.640911 43.05671

unclass(fixef(res))  ## actually a matrix of estimates with attribute "se"
## $orig
##         H04      C13
## pA 352.0025 460.0097
## pB 370.8997 494.5846
## pC 346.9318 430.8644
## pF 339.6614 429.4795
## pG 313.0000 376.4231
## pH 305.3889 376.9779
## pI 323.2885 404.6216
## pJ 343.8727 418.9064
## pK 335.4828 441.9861
## attr(,"se")
##          H04      C13
## pA  6.238914 13.64437
## pB 10.794693 19.86351
## pC 13.078774 25.54773
## pF  6.226796 12.55013
## pG 24.043034 48.31334
## pH 19.933367 43.42664
## pI 20.094619 43.61939
## pJ 19.856683 43.28562
## pK 19.640911 43.05671

str(ranef(res))
## List of 1
##  $ genetic: num [1:1525, 1:2] -6.02 -12.93 -10.16 33.51 6.77 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:1525] "19" "21" "23" "25" ...
##   .. ..$ : chr [1:2] "H04" "C13"
##   ..- attr(*, "se")= num [1:1525, 1:2] 23 22.8 23.6 23 23.6 ...
##   .. ..- attr(*, "dimnames")=List of 2
##   .. .. ..$ : chr [1:1525] "19" "21" "23" "25" ...
##   .. .. ..$ : chr [1:2] "H04" "C13"
##   ..- attr(*, "names")= chr [1:3050] "1" "2" "3" "4" ...
##  - attr(*, "class")= chr [1:2] "ranef.breedR" "breedR_estimates"

head(ranef(res)$genetic)
##           H04         C13
## 19  -6.016271   40.093547
## 21 -12.925035 -108.673107
## 23 -10.164449   23.276658
## 25  33.507715   80.855347
## 27   6.768289   -5.018311
## 29  22.201575   32.078520

Recovering the breeding values for each observation in the original dataset follows the same procedure as for one trait: multiply the incidence matrix by the BLUP matrix. The result, however, will be a matrix with one column per trait.

head(model.matrix(res)$genetic %*% ranef(res)$genetic)
##           H04        C13
## 151  5.923689  -6.612036
## 153  7.760706  22.486000
## 155 -7.414378 -38.978615
## 157  7.894009   3.756494
## 159  3.536361 -10.654445
## 161 12.431919  12.736590

Initial (co)variance specification

breedR will use the empirical variances and covariances to compute initial covariance matrices. But you can specify your own. This is particularly interesting for setting some initial covariances to 0, which indicates that you don't want that component to be estimated, and thus reducing the dimension of the model.

Typical cases are Multi-Environment Trials (MET, e.g. multiple sites, or years) where you don't really want to estimate the residual covariances, or when you know a priori that two traits are little correlated.

Specify the initial covariance values in matrix form.

initial_covs <- list(
  genetic = 1e3*matrix(c(1, .5, .5, 1), nrow = 2),
  residual = diag(2)   # no residual covariances
)
res <- 
  remlf90(
    fixed = cbind(H04, C13) ~ orig,
    genetic = list(
      model = 'add_animal', 
      pedigree = dat[, 1:3],
      id = 'self',
      var.ini = initial_covs$genetic),
    data = dat,
    var.ini = list(residual = initial_covs$residual)
  )

Some more features

Metagene interface

  • We have used simulated data from the metagene software

  • If you simulate data, import the results with read.metagene()

  • Use several common methods with a metagene object:

    • summary(), plot(), as.data.frame()

  • Plus some more specific metagene functions:

    • b.values(), get.ntraits(), ngenerations(), nindividuals(), get.pedigree()

  • And specific functions about spatial arrangement:

    • coordinates() extract coordinates
    • sim.spatial() simulates some spatial autocorrelation

Simulation framework

  • The function breedR.sample.phenotype() simulates datasets from all the model structures available in breedR

  • Limitation: only one generation, with random matings of founders

  • See ?simulation for details

Remote computation

If you have access to a Linux server through SSH, you can perform computations remotely

  • Take advantage of more memory or faster processors

  • Parallelize jobs

  • Free local resources while fitting models

  • See ?remote for details

Package options

  • breedR features a list of configurable options

  • Use breedR.setOption(...) for changing an option during the current sesion

  • Set options permanently in the file $HOME/.breedRrc

  • see ?breedR.option for details

breedR.getOption()
## $ar.eval
## [1] -0.8 -0.2  0.2  0.8
## 
## $breedR.bin
## [1] "/home/facu/Work/Proyectos/2013.T4F/bin/PROGSF90/linux/32bit"
## 
## $splines.nok
## determine.n.knots
## 
## $default.initial.variance
## default_initial_variance
## 
## $col.seq
## [1] "#034E7B" "#FDAE6B"
## 
## $col.div
## [1] "#3A3A98FF" "#832424FF"
## 
## $cygwin
## [1] "C:/cygwin"
## 
## $cygwin.home
## [1] "/home/facu"
## 
## $ssh.auth.sock
## [1] "/tmp/ssh-auth-sock-facu"
## 
## $remote.host
## [1] "eldorado"
## 
## $remote.user
## [1] "fmunoz"
## 
## $remote.port
## [1] 22
## 
## $remote.bin
## [1] "/home/fmunoz/R/x86_64-unknown-linux-gnu-library/3.0/breedR/bin/linux"
## 
## $ssh.options
## [1] "-x -o BatchMode=yes -o TCPKeepAlive=yes -e none"
Add a custom footer

BreedR functionality map

Clone this wiki locally